Сигнал -- это описание того, как один параметр изменяется от другого. Система -- это какой-то процесс, который дает выходной сигнал в ответ на входной.
| рис.1 Система -- любой процесс, который дает отклик y(t) на входной сигнал x(t) | |
Когда я буду говорить сигнал, то это означает просто математическая зависимость, без знания о том, что это такое: электрический сигнал, светимость люминофора или звук. Когда говорим о системе, точно также, опускаем детали, монитор это или телефон.
Системы бывают линейные и нелинейные. Чтобы понять то, что написано ниже на этой странице, чрезвычайно важно понять, что такое линейная система. Линейная система математически обладает двумя свойствами:
а) гомогеничностью (homogeneity): если амплитуду входного сигнала x(t) увеличить в k раз, то выходной сигнал y(t) увеличится тоже в k раз.
б) аддитивностью: если два входных сигнала поданные раздельно, вызывают отклики y1(t) и y2(t), то сумма x1(t)+x2(t) сигналов на входе дает точно y1(t)+y2(t). Не больше и не меньше.
Подобные оценки широко распостранены в инженерной и конструкторской практике. Пример линейной системы: ток в резисторе от напряжения.
| рис.2 Линейная система: процесс протекания тока через резистор в зависимости от приложенного напряжения |  |
Изменяя напряжение на выводах резистора, мы меняем ток через резистор по закону Ома: u=R*i. Закон, найденный Омом, гарантирует, что увеличение напряжения k*u обязано привести к увеличению тока в k раз. Пример нелинейной системы: тепло в резисторе от напряжения.
| рис.3 Нелинейная система: выделение тепла на резисторе в зависимости от напряжения |  |
Так как тепло, выделившееся в резисторе, растет по степенной функции u2, изменение в k раз напряжения u приведет к изменению в k2 выделившегося тепла.
Аддитивность можно представить как свойство системы не допускать "взаимодействия" между двумя сигналами. В звукотехнике, например, этот параметр используется для оценки качества усилителей: при подаче чистых синусоидальных сигналов система может показаться линейной, однако один сигнал, скажем, низкочастотный, может изменить параметры системы (усилителя) так, что другой сигнал, высокочастотный, окажется промодулирован низкочастотным и к тому же оба изменят свою синусоидальную форму— появится множество дополнительных гармонических сигналов. В итоге, простая сумма гармонических сигналов на входе приведет к искажению их формы и появлению дополнительных компонент на выходе. Такая система нелинейна. Вообще говоря, физических линейных систем не бывает, это математическая идеализация. Однако на каком-то интервале значений входных/выходных сигналов передаточную функцию при заданной точности можно представить линейной моделью.
Cathode Ray Tube (CRT) монитор -- система, в которой главную роль играет электронная лампа под названием кинескоп. Входной сигнал -- напряжение, выходной сигнал -- светимость.
Чтобы выяснить отклик системы, делают серию замеров напряжение-светимость. Конструктивные особенности электронной лампы таковы, что точки на графике, отображающие результаты замеров, ложатся на кривую степенной зависимости. Вы можете открыть любой справочник по электронным лампам и поискать графики анодно-сеточных характеристик триодов. На таких графиках будет представлена зависимость анодного тока от управляющего напряжения на сетке. В нашем случае светимость люминофора прямо пропорциональна анодному току. Вот наш система:
| рис.4 Нормированная зависимость интенсивности свечения монитора от напряжения видеосигнала на входном разъеме монитора |  |
Есть три мифа, гуляющие по интернету. Первый: нелинейность системы создает нелинейная светимость люминофорного покрытия [к примеру, 1]. Второй: закон нелинейности экспоненциальный. Оба утверждения ложны. На рисунке 4а показаны зависимости для трехэлектродной лампы [10]. Характеристика лампы обычно рассчитывается в приведенном виде, то есть в объединении всех напряжений, действующих на отдельных электродах. Миф третий -- гамма-коррекция компенсирует нелинейность зрительной системы человека.
| рис.4а Статические приведенные характеристики триодной лампы. В этих формулах: Ua– напряжение на аноде; Ug– напряжение на сетке; Rp—статическое внутреннее сопротивление лампы (от катода к аноду Ia/Ua); показатель степени n различен для различных участков характеристики и может принимать значения n=1-:-3; mu – коэффициент усиления лампы, m – ток начальной эмиссии. |  |
На заре телевизионной техники, когда парк телевизоров был еще незначителен, разработчики телевизионной сети встали перед задачей: линейный видеосигнал с видикона, поданный на вход телевизора, приводил к почти черной картинке, нужно вводить коррекцию сигнала, но на чьей стороне? Проще и дешевле на передающей, так как в те времена реализовать аппаратно такую коррекцию было дорого, и к тому же расточительно— пришлось бы встраивать такой корректор в каждый телевизор. Так и решено было ввести эти предыскажения на передающей стороне. Телевизоры оказались проще и дешевле. Коррекцию, которую ввели, называют "гамма". Миф третий: гамма— полезная функция в чем-то еще, кроме компенсации нелинейности монитора. Утверждение ложное. Сегодня это технический нонсенс. Подробное обоснование приведу ниже.
Рис. 5 Типичная цепь прохождения сигнала "освещенность в зависимости от пространственного расположения" от предмета до экрана монитора. [2].
Пояснения к рис. 5., слева направо. Будем говорить о самере, использующей матрицу ПЗС (CCD).
а) Зависимость напряжение ПЗС (CCD) от освещения монохромным светом— чрезвычайно линейна. Принцип действия -- светоинтегрирующее устройство. Линейность [свет–ПЗС–напряжение] обеспечивается линейностью накопления заряда и линейностью считывания элемента.
б) Наибольшие проблемы у матриц ПЗС в темновой области— именно в этой части к выходному сигналу матрицы суммируется шум. На рисунке 5: sensor noise.
в) непрофессиональные камеры имеют неотключаемое устройство, на рисунке 5 обозначенное как compressor. Профессиональные устройства позволяют получать RAW-image, то есть данные с матрицы без предыскажений.
г) следующий источник шума, показанный на рисунке— шум дискретизации, шум электронных схем, схем сжатия и кодирования сигнала (JPEG), image noise.
д) Тракт переноса данных. Представлен как "черный ящик" storage, transmission, processing,... Сюда можно отнести кабель, устройства памяти, программы редактирования и т.п.
е) далее, собственно, дисплей, с передаточной функцией, представленной на рис. 4
На сегодняшний день линеаризовать передаточную функцию монитора не составляет проблем. Если считать видеокарту компьютера составной частью монитора (то же самое показано на рис.5— expander есть LUT видеокарты), то становится ясно, что такой анахронизм, как предыскажение сигнала в самом начале тракта есть просто дань истории.
Прежде чем говорить о линеаризации, нужно знать характеристику системы. Вообще говоря, для этого пришлось бы сформировать набор напряжений на входе монитора и измерить фактический отклик. Обычно же считается, что монитор достаточно точно следует по форме кривой степенной функции, а степень (гамма) имеет значение 2.5 для каждой пушки (исследование лаборатории Би-Би-Си в этом вопросе, правда, заканчивается утверждением, что гамма зависит от установки уровня черного, однако это вопрос уже методики измерения, а не конструктивно определенной величины. К примеру, нормально спроектированное устройство калибровки и профилирования мониторов обязательно предложит установить уровень черного и белого, перед самим процессом калибровки). Отклонения гаммы составляют примерно плюс-минус 0.25. Уже отсюда видно, что без конкретного промера мы можем расчитывать лишь на приближенное соответствие формулы рис.4 конкретной характеристике монитора.
| рис.6 Слева: кривая с рис.4, справа т.н. гамма-компенсация, как правило, "вшитая" в файлы изображений. |  |
| рис.7 Так выглядит нормализованный график суммы двух функций f(u)+f-1(u), физический смысл: эта кривая показывает скорость изменения приращения аргумента (u) относительно линейного приращения. |
 |
Солидные источники, такие как [3], указывают несколько иные компенсационные кривые, см. рис.8.
рис.8 HDTV Standard предлагает иную кривую для компенсации нелинейности монитора (предыскажений на передающей стороне). Здесь R это linear-light intensity а R'709 это нелинейность монитора, см. рис.4 Как видим, при малых сигналах степенная функция заменена на отрезок прямой.  |
 |
Кстати, нет единого мнения, почему при хорошо известной кривой монитора PC (рис.4) с гаммой 2.5 для "компенсации" выбрана 1/2.2. Чаще всего это связывают с тем, что поскольку гамма-компенсация пришла из TV, то в расчет берется неблагоприятные условия просмотра при достаточно ярком окружающем освещении. Потребитель при сильном освещении комнаты, где стоит телевизор, просто прибавляет регулятором яркости общую яркость телевизионной картинки, при этом повышается уровень черного, но самые светлые места попадают в нелинейную область из-за ограничения тока катода кинескопа (а соответственно току, яркости свечения люминофора). Зависимость нелинейности телевизора перестает соответствовать степенной функции по форме, при этом степенная функция 2.2 обеспечивает меньшую среднеквадратичную ошибку аппроксимации. Совершенно ясно, что такое значение гаммы не может компенсировать нелинейность монитора, настроенного правильно по уровню черного, из-за другой формы кривой. Значение гаммы 1/1.72, принятое для рабочего пространства Макинтошей, может сбить с толку, если не знать, что вторая, недостающая часть до 1/2.5, уже применена к монитору. Таким образом, компенсация нелинейности разбита на две части — в рабочем пространстве, и в мониторе (к монитору я отношу и видеокарту). Выбор меньшего значения для гамма-компенсации в рабочем пространстве уменьшает искажения в обработке изображений. Поэтому система Макинтош принципиально лучше, чем PC, позволяет подготовить изображения в области теней, если говорить о начальных установках, предложенных для этих систем производителями. Об этом позже.
На сегодняшний день стало нормой использовать калибраторы монитора в профессиональной работе.
Как правило, во многих статьях даются советы, в которых заметно незнание авторами, теперь уже почти забытой, теории ламповой техники. Но писать что-либо и давать советы для мониторов, не зная этой теории, нонсенс. Прежде чем калибровать монитор, исключительно важно установить рабочую точку анодно-сеточной характеристики нашей лампы-кинескопа (в более общем виде можно посмотреть [11]). Известно, что ламповые выходные каскады по расположению рабочей точки (применительно к монитору, это уровень яркости черного) классифицируются на типы A, AB, B, BC, C. Работа кинескопа относится к режиму работы AB или B, в зависимости от того, где находится рабочая точка. В переводе на понятный язык, в зависимости от того, имеет ли монитор начальный уровень засветки. Чтобы узнать, какую расчетную яркость черного закладывали конструкторы, лучше всего попробовать поискать информацию на сайте производителя, но в общем случае это будет 0.02-0.07. Уровень черного устанавливается регулятором Brightness. Если вы установите слишком большую начальную яркость для черного, -- это может понадобится для работы в сильно освещенном месте, -- понятие "гамма" может оказаться не применимым к нелинейной функции светоотдачи вашего монитора. Такая нелинейность сильно будет отличаться от степенной функции (рис.6, слева).
Например, вот кривые моего монитора:
 |
| рис.9 Черная линия с точками -- идеальная характеристика монитора. Синяя линия (target) — заданная пользователем гамма (для моего монитора ViewSonicP810 gamma=2.54). Компенсационные значения, точно компенсирующие характеристику монитора в степенную функцию (синия линия)-- цветные линии около черной линии. Цветовая температура для калибровки указана D65. |
Как видим, калибратор не приводит к линейности монитора (за исключением случая калибровки в гамму 1.0). Это миф номер четыре. Вычисленные на основе измерений с экрана с помощью серии промеров градационой шкалы серого поля значения, загружаемые в LUT видеокарты, приводят всего лишь кривую зависимости Output Luminance к точной степенной зависимости от Input RGB. Это синия линия Target на рис.9. А точную степенную зависимость призвана компенсировать гамма-функция, чего на самом деле, в случае применения гаммы=2.2, не происходит. Точно компенсирует эту зависмость только та гамма, в которую происходила калибровка монитора, в моем случае 2.54. Откуда взялось "странное" значение гаммы, выбраной мной?
Для примера я "откалибровал" свой монитор для гаммы 2.2. Как видим, родная гамма моего монитора явно не 2.2, потому как программное обеспечение калибратора пытается загрузкой коэффициентов в LUT видеокарты привести кривую светоотдачи к правильной степенной зависимости, и делать это приходится большими корректировочными коэффициентами. Вообще говоря, математически правильно было бы корректировать нелинейность монитора в гамму 1.0, то есть, синия линия Target на рис.10 должна совпасть с черной, а цветные кривые могут разъезжаться как им угодно. Но во-первых, это уже будет называться не калибровкой, а линеаризацией. Во-вторых, из-за сегодняшних ограничений 8-битных видеокарт мы получим очень большие ошибки дискретизации [4]. Математическая модель в этом случае имеет свои ограничения, и на этапе калибровки следует придерживаться конструктивных параметров мониторов. В будущем, когда появиться видеопроцессоры 12 бит (этого достаточно) реального времени, и не дороже какого-нибудь таймера 555, мониторы станут линейными от входного разъема до светимости люминофора. При этом видеокарта перейдет из компьютера туда, где ей положено быть по функциональному назначению — в монитор.
 |
| рис.10 Черная линия с точками -- идеальная характеристика монитора. Синяя линия (target) — заданная пользователем gamma=2.2. Компенсационные значения, точно компенсирующие характеристику монитора в степенную функцию (синия линия)-- цветные линии около черной линии. |
Как видим, все три пушки монитора ведут себя почти одинаково. Причина этого в том, что современные вещества для люминофоров имеют родную цветовую температуру белого около 9000K, и если монитор достаточно хорошего качества (мое мнение), то выбор цветовой температуры не ниже 6500K не должен приводить к сильной разбалансировке по каналам R,G,B. При калибровке в D50 кривые могут разъехаться так, что площадь под ними может доходить до 1/4 от всего графика. На рис. 11 пример калибровки в D50 при gamma=2.2.
 |
| рис.11 Черная линия с точками -- идеальная характеристика монитора. Синяя линия (target) — заданная пользователем gamma=2.2. Цветовая температура для калибровки указана D50. Компенсационные значения, точно компенсирующие характеристику монитора в степенную функцию (синия линия) -- цветные линии около черной линии. |
Как видим, с математической точки зрения, для идеальной видеокарты прошел вполне нормальный процесс аппроксимаций заданных функций. Реально же, из-за ограничений 8-битной видеокарты -- ошибки, возможно, выйдут за допустимые границы для профессиональной работы. Дело в том, что если потеря для монохромного изображения составляет три градации, то в цветном это уже 3*3*3=27.
При калибровке в родную гамму (она смотрится в *.icm profile от производителя, можно оценить и по минимуму расхождений цветных линий от линейной черной— как на рис.9,10,11; можно пользоваться и специальными тестовыми картинками— но это отдельная тема) и в температуру не ниже 6500, действительно высококачественный монитор будет иметь минимальные корректировки по всем каналам. Соотвественно, и самый широкий цветовой охват. У производителей всё, что сказано в этом пункте, обычно спрятано за фразой: «рекомендуется проводить калибровку при такой-то гамме в такую-то температуру, при этом достигается максимальная производительность устройства.» Калибровать во что-либо иное, чем в родные конструктивные параметры— значит сознательно или бессознательно, но уменьшать гамут (gamut— цветовой охват) монитора и вводить дополнительные ошибки дискретизации в ЦАПе видеокарты (при 8 битах они точно есть, смотрите [4]). При работе с ICM-aware приложением, поддерживающим не менее 12-битную обработку файлов, сегодня калибровка во что-либо иное, чем в конструктивно заложенное, полная бессмыслица. Гамма-функция у монитора, если ее подтянули калибровкой к степенной, может быть очень точно скорректирована с минимальными ошибками дискретизации для любого файла внутри такого приложения, при условии, что вы сделали доступным для этого приложения профиль для вашего монитора.
Кроме сказанного о технической стороне калибровки, нужно предупредить о возможном недоразумении относительно термина "калибровка". Редкий случай, когда собеседники договариваются о едином понимании всех терминов перед началом дискуссии. Общепринятое соглашение для калибровки, относительно нашей темы, есть примерно следующее: калибровка— приведение устройства в то состояние, в котором оно соответствует техническому заданию при изготовлении на заводе-изготовителе (математической модели в конструкторских расчетах). В этом смысле калибровка некоторых устройств, например, недорогих принтеров, будет заключаться в проверке наличия бумаги в лотке и нажатого состояния кнопки "сеть". Все остальные операции и манипуляции могут носить название линеаризация и характеризация (профилирование).
Множество приборов и устройств собирают и отображают для человека сигналы. Математически они описываются функциями, и математически всё выглядит очень гладко. Однако физическая реализация некоторых передаточных, корректирующих, линеаризующих и т.д. фильтров упирается в то, что математические функции отыскиваются в самих электронных приборах, например, логарифмическая функция есть одна из физических зависимостей в транзисторе, включение которого в определенный контекст схемы даст логарифмическую функцию у этой схемы. Однако эта зависимость у транзистора лишь аппроксимация (приближение) математической. Функции умножения сигналов в аналоговой технике— сплошная головная боль конструкторов и инженеров, применяют ее только там, где без этого уже никак не обойтись. Для человека, знакомого с математикой, умножение двух функций не выглядит чем-то особенным. Применение математики в исследовании сигналов глубоко разработанная тема, и была таковой задолго до эры цифровой техники. Математика изучает числа. Поэтому перевод сигналов в поток чисел (наглядно— это как бы следующие друг за другом таблицы чисел, описывающие сигнал интервал за интервалом) позволяет мыслить об обработке, распознавании, сжатии, генерации речи, музыки и т.д. в контексте математики. В конце концов, сетчатка нашего глаза— дискретное устройство, состоящее хоть и из большого, но конечного числа колбочек и палочек. Вопрос о том, почему мы воспринимаем мир не дискретно, каков механизм ощущения слитности образов, запахов (наш нос может различать концентрации некоторых веществ буквально в сотни молекул на кубический сантиметр), звуков — будущая задача исследователей.
От видеокарты компьютера к монитору на вход подаются ступеньки напряжения по каждому каналу: R,G,B. На выходе монитора— светимость точек люминофора. В идеале ступеньки напряжения на входе монитора соответствуют числам в файле. Если у нас 8-битное изображение, для каждого канала RGB имеется 256 возможных значений ступенек.
| рис.12 Каждая ступенька напряжения, подаваемая на вход, в идеале представляет собой число в файле (для простоты будем говорить о grayscale файле) В синем кружке — обратная операция аналог->цифра. |
 |
Наши числа для монитора представляют ту же кривую рисунка 4. В линейной системе каждому числу 0...255 из файла соответствует ступенька на входе и ступенька на выходе. Для монитора эти 256 ступенек означают 256 градаций светлоты (светимости). В нелинейной системе ступеньки будут разными как по высоте, так и по ширине, что приведет к уменьшению степеней градации. Мы подразумеваем, что на вход всегда подаем 256 одинаковых по высоте ступенек напряжения. Итак, мы отправили на монитор лесенку из 256 градаций, сколько градаций мы увидим на мониторе? Чтобы это выяснить, посмотрим на график зависимости и на таблицу значений.
| рис.13 График зависимости светимости люминофора от дискретного напряжения на разъеме монитора |  |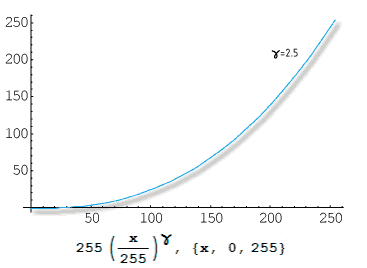
Таблица того, что происходит на мониторе при подаче на него равномерных линейных отсчетов дискретного сигнала, приведена в таблице ниже. Увеличение напряжения последовательно от 0 до 20 ступенек приводит всего лишь к одной ступеньке расчетной светимости экрана. Дальше хорошо видно, что 46 ступенек на входе приводят к увеличению светимости всего на 3 расчетные ступеньки.
Выход Вход --------------------- 0.0 0 ---------\ 0.0002455781533 1 ---- \ 0.0013891998204 2 ---- \ 0.0038281845497 3 ---- \ 0.0078585009077 4 ---- \ 0.0137282361179 5 ---- \ 0.0216554820380 6 ---- \ 0.0318371973407 7 ---- \ 0.0444543942545 8 ---- \ 0.0596754912681 9 ---- \ 0.0776586308216 10 ---- = 0 0.0985533615625 11 ---- / 0.1225019055917 12 ---- / 0.1496401414724 13 ---- / 0.1800983850686 14 ---- / 0.2140020220908 15 ---- / 0.2514720290475 16 ---- / 0.2926254083801 17 ---- / 0.3375755563705 18 ---- / 0.3864325775293 19 ---- / 0.4393035557734 20 ---------/ 0.4962927902822 21 0.5575020021566 22 -------\ 0.6230305167077 23 ---- \ 0.6929754252173 24 ---- \ 0.7674317292710 25 ---- \ 0.8464924701832 26 ---- \ 0.9302488455870 27 ---- = 1 1.0187903149024 28 ---- / 1.1122046951146 29 ---- / 1.2105782480647 30 ---- / 1.3139957602712 31 ---- / 1.4225406161459 32 -------/ 1.5362948653469 33 -----\ 1.6553392849045 34 ---- \ 1.7797534366721 35 ---- \ 1.9096157205796 36 ---- = 2 2.0450034241061 37 ---- / 2.1859927683391 38 ---- / 2.3326589509390 39 ---- / 2.4850761862943 40 -----/ 2.6433177431168 41 ----\ 2.8074559797005 42 ---- \ 2.9775623770421 43 ---- / = 3 3.1537075700006 44 ---- / 3.3359613766549 45 ----/ 3.5243928260017 46 3.7190701841224 47 3.9200609789347 48 4.1274320236345 49 4.3412494389220 50 4.5615786740995 51 4.7884845271192 52 5.0220311636520 53 5.2622821352445 54 5.5093003966227 55 5.7631483221978 56 6.0238877218256 57 6.2915798558645 58 6.5662854495763 59 6.8480647069082 60 7.1369773236938 61 7.4330825003054 62 7.7364389537908 63 8.0471049295208 64 8.3651382123785 65 8.6905961375109 66 9.0235356006703 67 9.3640130681637 68 9.7120845864337 69 10.067805791287 70 10.431231916793 71 10.802417803858 72 11.181417908509 73 11.568286309881 74 11.963076717940 75 12.365842480939 76 12.776636592629 77 13.195511699236 78 13.622520106209 79 14.057713784751 80 14.501144378151 81 14.952863207909 82 15.412921279679 83 15.881369289031 84 16.358257627039 85 16.843636385699 86 17.337555363196 87 17.840064069014 88 18.351211728896 89 18.871047289673 90 19.399619423945 91 19.936976534648 92 20.483166759479 93 21.038237975213 94 21.602237801901 95 22.175213606956 96 22.757212509129 97 23.348281382388 98 23.948466859692 99 24.557815336672 100 25.176372975218 101 25.804185706973 102 26.441299236752 103 27.087759045862 104 27.743610395353 105 28.408898329188 106 29.083667677333 107 29.767963058785 108 30.461828884518 109 31.165309360365 110 31.878448489838 111 32.601290076879 112 33.333877728553 113 34.076254857674 114 34.828464685384 115 35.590550243668 116 36.362554377811 117 37.144519748815 118 37.936488835752 119 38.738503938072 120 39.550607177864 121 40.372840502068 122 41.205245684640 123 42.047864328680 124 42.900737868505 125 43.763907571689 126 44.637414541064 127 45.521299716671 128 46.415603877682 129 47.320367644284 130 48.235631479520 131 49.161435691100 132 50.097820433180 133 51.044825708097 134 52.002491368084 135 52.970857116944 136 53.949962511697 137 54.939846964197 138 55.940549742717 139 56.952109973509 140 57.974566642331 141 59.007958595952 142 60.052324543628 143 61.107703058548 144 62.174132579268 145 63.251651411100 146 64.340297727496 147 65.440109571398 148 66.551124856565 149 67.673381368885 150 68.806916767656 151 69.951768586853 152 71.107974236368 153 72.275571003233 154 73.454596052826 155 74.645086430051 156 75.847079060500 157 77.060610751604 158 78.285718193755 159 79.522437961420 160 80.770806514229 161 82.030860198050 162 83.302635246051 163 84.586167779740 164 85.881493809989 165 87.188649238046 166 88.507669856532 167 89.838591350417 168 91.181449297991 169 92.536279171808 170 93.903116339631 171 95.281996065347 172 96.672953509886 173 98.076023732108 174 99.491241689696 175 100.91864224002 176 102.35826014099 177 103.81013005194 178 105.27428653439 179 106.75076405295 180 108.23959697608 181 109.74081957688 182 111.25446603394 183 112.78057043205 184 114.31916676303 185 115.87028892642 186 117.43397073028 187 119.01024589191 188 120.59914803858 189 122.20071070823 190 123.81496735020 191 125.44195132591 192 127.08169590957 193 128.73423428886 194 130.39959956557 195 132.07782475630 196 133.76894279309 197 135.47298652407 198 137.18998871413 199 138.91998204550 200 140.66299911840 201 142.41907245166 202 144.18823448331 203 145.97051757118 204 147.76595399351 205 149.57457594952 206 151.39641555998 207 153.23150486781 208 155.07987583860 209 156.94156036121 210 158.81659024830 211 160.70499723686 212 162.60681298878 213 164.52206909134 214 166.45079705780 215 168.39302832782 216 170.34879426808 217 172.31812617269 218 174.30105526378 219 176.29761269192 220 178.30782953665 221 180.33173680696 222 182.36936544175 223 184.42074631033 224 186.48591021285 225 188.56488788082 226 190.65770997750 227 192.76440709842 228 194.88500977175 229 197.01954845881 230 199.16805355449 231 201.33055538766 232 203.50708422162 233 205.69767025452 234 207.90234361976 235 210.12113438644 236 212.35407255974 237 214.60118808134 238 216.86251082982 239 219.13807062106 240 221.42789720860 241 223.73202028410 242 226.05046947765 243 ----\ 228.38327435820 244 ----/ 230.73046443390 245 233.09206915253 246 235.46811790180 247 237.85864000977 248 240.26366474517 249 ----\ 242.68322131781 250 ----/ 245.11733887887 251 247.56604652130 252 250.02937328017 253 252.50734813297 254 255.0 255
Внизу таблицы поведение меняется на обратное: здесь ступенька на входе приводит к увеличению отдачи монитора в среднем на 3 ступени. Итого, в самой темной части мы теряем градации светлоты, потеряв в тенях около 60 градаций, а в самой светлой теряем плавность переходов. В итоге, мы остаемся примерно со 190 градациями, и при том еще имеем неравномерность в светлой части. Всё это, как мы помним, для 8-битной видеокарты.
Мы отправили на монитор 256 градаций, сколько градаций мы увидим на мониторе? Именно, сколько увидим? Сколько градаций получим измерив, уже ясно.
Существует много мнений на этот счет. Например, "an engineer with 25 years experience in color science and digital imaging" Bruce Justin Lindbloom считает, что некий Dan Margulis :) неправ [5]. Дэн утверждает, что 8 бит -- вполне адекватный формат для натуральных изображений (сканированные и фотографические). Для компьютерных изображений (Computer Generated Image, CGI) действительно, приходится использовать 16 бит.
Выберите самый качественный и самый чувствительный, на ваш взгляд, файл изображения из своей коллекции и создайте три копии в Фотошопе: 256, 92, 64 градации, применив постеризацию (menu: Layer>New Adjastmens Layer>Posterize). Согласитесь, что в натуральном изображении совершенно достаточно более 64 уровней градаций. Значит, не всё так плохо с нашим монитором? Попробуйте теперь сделать длинную растяжку черного цвета (min 1600px, и не забудьте отключить dither) и примените постеризацию в 256 градаций, и теперь станет ясно, полосатость (banding) -- неотъемлимая часть CGI. Почему?
Наше зрение ищет границы. Если в CGI слишком гладкие, математически-непрерывные, переходы, зрение будет реагировать на малейшие изменения яркости соседних участков. Человек очень хороший нуль-метр. Затрудняясь ответить, насколько разные по светлоте два участка, он очень хорошо справляется с задачей определения соответствия двух соседних участков друг другу. Ниже представлен градиент при постеризации в 50 градаций, что соответствует полоскам по светлоте через 2%. Полосы видны совершенно ясно. (кстати, если на Вашем мониторе некоторые полоски видны окрашеными, это означает, что монитор не откалиброван. Первый признак калиброванного монитора -- изумительный, действительно серый градиент).
| рис.14 Градиент черного в 50 градаций. Конечно, насколько равномерно выглядят градации, зависит от того, как ваш монитор калиброван. То есть, насколько точно каждая пушка дает электронный луч для получения равных пропорций светимости R,G,B и насколько точно их сумма следует степенной функции. Это изображение гамма-компенсировано для монитора с gamma=2.5 |  |
Однако применение слоя Posterize со значением 50 к натурным фотографиям доказывает правоту Dan Margulis: реальные изображения нечувствительны к сокращению числа градаций. В зависимости от сюжета, исходя из моего опыта, по критерию "заметность" допустимо снижение градаций от 112 до 36. Кстати, если вы поэкспериментируете с десятком фотографий, возможно, заметите, что некоторые, при сокращении градаций, субъективно выглядят даже "лучше" оригинала. Визуально это совпадает с тем, как будет выглядеть фотография, нуждающаяся в незначительном исправлении с помощью окна Curves.
Первый вывод: 8 бит видеокарты и 190 градаций монитора более чем достаточны для слитного показа некомпьютерных изображений. Для изображений, генерированных математически, нужны 12 бит видеокарты. Digital Betacam, используемый в high-end студиях, использует 10 бит на канал, и также 10 бит является стандартом для некомпрессированных видеопотоков в Serial Digital Interface (SDI).
Нам придется рассмотреть целый ряд вопросов по физиологии, свойствам зрительного восприятия и построить модели по результатам известных экспериментов. Здесь же рассмотрим способы получения цифровых изображений, рабочих пространств (выбор математического поля) и их оценку.
Конечно, здесь не будет рассматриваться весь огромный материал, претендующий на размещение под таким заголовком. Останемся в контексте вопроса о гамма-мифологии и рассмотрим содержательную сторону недоразумений, неправильных пониманий и ошибочных представлений.
В 1942 году трое ученых Hecht, Schlaer & Pirenne провели эксперимент для ответа на вопрос, какова предельная чувствительность глаза в идеальных условиях? [7]. То, что они обнаружили, оказалось весьма неожиданным, поэтому опишем классический эксперимент. Описание этого эксперимента затрагивает фундаментальные принципы работы зрительной системы.
Основа эксперимента очень проста — экспериментаторы предъявляли в качестве стимула вспышки света в поле зрения испытуемого и определили минимальный уровень света. Но прежде чем поставить эксперимент, им пришлось ответить на следующие вопросы:
Мы знаем, что нашему зрению нужно некоторое время, чтобы привыкнуть к темноте. Однако сколько времени? Минута? Две? Три часа? Десять часов? Ответ на этот вопрос на рис. 15.
| рис.15 Темновая адаптация глаза |  |
В этом эксперименте за время адаптации принято 40 минут.
К следующему вопросу, где должен быть расположен в поле зрения испытуемого источник вспышек, ответ показан на рис.16. Из этого рисунка видно, что максимальная чувствительность глаза находится в стороне от центральной ямки, так, что направление взгляда на объект должно составлять 20 градусов от самого направления на объект. Это известно с давних пор, когда люди изучали небо невооруженнм глазом. Еле заметную звезду можно было яснее фиксировать, если смотреть не прямо на нее, а чуть в сторону. Однако в какую сторону нужно отводить взгляд, чтобы не попасть на слепое пятно (место, где находится центральный нервный ствол)?
рис.16 Распределение палочек на сетчатке. На горизонтальной оси точка 0 совмещениа с центральной ямкой. |
 |
Направление на источник и правильное направление фиксации взгляда показаны на рис.17.
 |
| рис.17 Правильное расположение источника световых вспышек относительно правого глаза. Вид сверху. |
Размер светового пятна был выбран 10 минут, так как было известно, что от 10 минут и меньше размер светового пятна не играл роли (spatial summation and Ricco’s law).
Продолжительность предъявления стимула была выбрана 1 миллисекунда (temporal summation and Bloch’s law).
Цвет света выбран 510 нм — зеленый, на основе известной кривой, см. ColorData.html (scotopic vision). Интересный вопрос, как была установлена такая зависимость? Сложность здесь в том, что совершенно разные по цвету световые стимулы нужно различить по светлоте, но разные по цвету стимулы человек сравнивает неудовлетворительно. Вновь напомню, что суждение человека "насколько светлее" очень сильно варьируется день ото дня, от количесва выпитого кофе и неспаных ночей. Однако способность человека выступать "нуль-метром" очень стабильна. В случае с разноцветными, бок о бок стимулами, детектирование нуля, баланса, светлоты, не работает. Поэтому комиссией CIE были приняты эксперименты, основанные на методе, подобном для демонстрации стробоскопического эффекта. Называется он фликер-метод (flicker photometry). Наблюдатель смотрит на экран с двумя представленными бок о бок образцами световых пятен. Пятна переключаются попеременно, с частотой примерно 15 Герц -- зрелище, надо сказать, пренеприятное :). Частоту слегка подстраивают, чтобы перемигивания цветами стали менее заметными, и проступил эффект от смешивания цветов, то есть, к примеру, зеленый и красный дали желтый; но сам фликер-эффект от желтого оставался заметным. Затем подстраивают мощности источников света до исчезновения (минимизации) фликер-эффекта, когда человек видит стабильный смесевой цвет. В этот момент считают, что те же световые пятна, светящие постоянно, дают равную светлоту.
Результат эксперимента определения чувствительности глаза: при условиях, перечисленных выше, глаз детектирует 90 фотонов. Даже сегодня изготовление таких детекторов сопряжено с большими трудностями (не имеются в виду аналоги счетчика Гейгера, но датчики с линейной характеристикой в диапазоне хотя бы трех порядков). Однако 90 фотонов — это весь свет, пришедший к оптической системе глаза, при этом:
Оставшиеся 10 фотонов и есть реальная чувствительность палочек.
Заметим, что у нас нет проблем видеть лист бумаги белым как при солнечном свете, так и при свете звезд безоблачным небом. Разница в освещенности сетчатки при этом равна отношению:
светимость листа белой бумаги под прямым солнечным светом равна 10тыс. нит;
светимость под звездным небом 0.00001 нит. Так как нужно учесть автоматическую работу зрачка, учтем диаметр отверстия, сквозь которое свет проходит к сетчатке:
диаметр зрачка для листа под солнцем 2мм, откуда площадь зрачка Pi*r2=3.14мм2.
диаметр зрачка для листа под звездами 8 мм, откуда площадь зрачка Pi*r2=50мм2.
Освещенность сетчатки от белого листа под солнцем равна 10000нит*3.14мм2=31400 троланд (единица в медицинской оптометрии)
Освещенность сетчатки от белого листа под звездами 0.0001нит*50мм2=0.005 троланд
Отношение освещенностей сетчатки: 31400/0.005=6.3миллиона раз.
В целом же человеческое зрение оперирует с объектами, светимость которых относится как 1 к 10 миллиардам.
Посмотрим, как создаваемые человеком приборы оперируют с диапазоном яркости.
Оптическая плотность D -- это десятичный логарифм отношения, которое называют либо коэффициент отражения, либо коэффициент пропускания. Чтобы наглядно представить, что такое D, ниже представлена табличка соответствия:
| оптическая плотность D |
непрозрачность | прозрачность |
| 1 | 10 | 1/10 |
| 2 | 100 | 1/100 |
| 3 | 1000 | 1/1000 |
| 4 | 10 000 | 1/10 000 |
| 5 | 100 000 | 1/100 000 |
| 6 | 1 000 000 | 1/1 000 000 |
 |
| рис.18 Аналогия работы глаза и фотокамеры для объяснения темновой адаптации. |
Фотоаппарат при съемке объектов на сцене имеет записанные яркости оптического изображения на обычной фотопленке, которые переносятся на фотобумагу, и бумага имеет оптическую плотность поверхности не более 2 (практически предельная оптическая плотность поверхности у черного меха — 2.4). В то же время, обычная сцена имеет плотность яркостей 6D. К примеру, фотокамера на рис.18 имеет следующие возможности для "адаптации":
У нашего зрения нет возможности изменить время экспозиции, сетчатка освещается непрерывно. Мы не можем поменять пленку (сетчатку), это тоже понятно. Остается изменение диаметра входного отверстия, зрачка. Расчет, подобный уже проделанному, показывает, что освещенность сетчатки при изменении зрачка от 2 до 9 мм изменяется всего лишь в 20 раз. В сравнении с десятью миллиардами это ничто. Основная доля адаптации базируется на разделе в оперировании освещенностью между двумя типами фоторецепторов: т.н. палочек и колбочек. Палочки слепы к цвету и обеспечивают фотонную чувствительность в темноте (scotopic system). Колбочки отвечают за восприятие цвета и работают в следующем диапазоне яркости (photopic system). Диапазон работы обеих систем слегка перекрываются, так что возможен такой подбор освещенности сцены, когда будут работать оба типа фоторецепторов. Дальнейшее объяснение темновой адаптации состоит в предположении, которое называется фотохимическое объяснение. Его суть состоит в том, что обесцвеченый пигмент (пигмент вступает в химреакцию, запуская процесс рождения сигнала, при этом сам обесцвечивается) регенерирует в первоначальное состояние. При этом расчеты показывают, что восстановившийся на 50% родопсин (пигмент сумеречного видения) должен увеличить порог чувствительности в 10млн. раз. Однако это остается гипотезой, так как эксперименты по восстановлению 50% родопсина показали, что порог изменяется в 1000 раз сильнее. Объяснения этому пока нет.
Точно так же, как наше зрение адаптируется к темноте, восстанавливая максимальную чувствительность, очевидно, что такая же способность существует к восстановлению нормального зрения при переходе от темноты к свету. Теперь, наконец, мы подобрались к очень важному, в контексте нашей темы, эксперименту.
Световая адаптация изучается измерением способности испытуемого к возможности обнаружения слабого светового сигнала на светлом фоне. В самом начале испытуемый находится в полной темноте, пока не произойдет темновая адаптация. Затем появляется освещенный экран как фон и испытуемому дают время на адаптацию к посветлевшему фону. Адаптация к свету проходит значительно быстрее, чем к темноте, обычно за 1.5 минуты. На этом фоне проецируют светлое пятно увеличивающейся яркости, и как только испытуемый фиксирует появление пятна, производится отсчет физической величины яркость (luminance) (кд/м2) для фона и для пятна. Процесс продолжается, пока не будет достигнут предел болезненной яркости фона.
В первых экспериментах на основании полученных результатов определилась зависимость [8]:
, где
L – величина изначальной яркости;
дельта L – величина приращения яркости порога различения;
Эта зависимость носит название закон Вебера (Weber's law). Более точные повторные эксперименты выявили некоторую неравномерность, которую не описывал закон Вебера.
| рис.19 Световая адаптация глаза. |  |
Секция 1: Почти черный фон, нейронный шум сетчатки определяет первое приращение дельта(I).
Секция 2: очень слабо освещенный фон, видимые флуктуации фона определяют уровень приращений. Эту часть описывает закон DeVries-Rose, по которому приращение дельта(I) возрастает как корень квадратный от яркости Ib.
Секция 3: длинная секция (10 000раз) с наклоном примерно 1. Из этого результата прямо следует, что приращение дельта(I) возрастает прямо пропорционально яркости фона и его точно описывает математическое выражение с названием закон Вебера (Weber's law). Постоянная k называется постоянной Вебера. Для палочек эта постоянная примерно равна 0.14. Это означает буквально: если фон имеет яркость 100ед, детектируемое приращение будет 14ед; если фон имеет 1000ед, приращение будет 140ед. Это самый главный принцип человеческого зрения. Глаз и мозг сконструированы так, что главным образом отмечают разницу в яркости, почти игнорируя абсолютную яркость. Светлота (lightness) на этом участке почти не зависит от свойств самого света. Допустим, мы держим в руках белый лист бумаги с черным шрифтом при освещенности, соответствующей самой нижней части секции три. Запомним яркость черной краски. Затем выше, в конце секции три, мы по-прежнему видим точно тот же черный текст на белой бумаге. Но на этот раз яркость черной краски такова, какая была у белой бумаги в начале секции. Тем не менее, бумага выглядит белой, а текст выглядит черным. В то же время, увеличение приращения, нужного для уверенного обнаружения, возрастает с увеличением яркости фона, что означает уменьшение чувствительности глаза. Это необходимо для нашего зрения, чтобы продолжать эффективно работать.
Секция 4: Резкий излом — результат построения графика в осях log/log. На самом деле, в линейных осях все происходит плавно, зато в линейных осях практически не разглядеть секции 1 и 2. Вообще, я постарался не давать здесь логарифмических осей, так как человек, никогда не работавший, скажем, с Децибелами (это не медицинский термин, а технический:), не сможет понять физического смысла в поведении кривой на графике. Однако здесь всё объяснено покусочно, поэтому появление такого графика не должно вызвать кривого толкования. Секция 4 показывает момент, когда палочки при работе со светом начинают входить в режим насыщения, кстати, насыщению соответствует всего 10% обесцветившегося родопсина. В тот же момент начинают работать колбочки, которые тоже дают свой вклад в ощущение светлота (lightness). Обратите внимание: физически ничего не происходит с нашими фоном, и стимулом, в виде пятна света на фоне. Равномерное приращение физической величины яркость (luminance) на этом участке приводит к неравномерному ощущению светлота (lightness). Еще раз подчеркну: прямой связи между физическими величинами и ощущением нет. Этот участок заканчивает сумеречное (scotopic) бесцветное зрение и появляется ощущение цвета. Вначале самыми светлыми покажуться синие предметы (Purkinje Shift or Purkinje Phenomenon).
Секция 5: Это полностью колбочковое, цветное, зрение (photopic system). Здесь снова результаты описываются законом Вебера, с другим коэффицентом: 0.015. Этот участок продолжается до самого конца.
Наиболее важный момент: секция 3 и секция 5 имеют наклон 45 градусов. В осях log/log это возможно, если приращение ощущения светлота есть постоянное отношение физической величины яркость фона к значению приращения яркости. Это и есть закон Вебера. Если в линейных осях наклон прямой линии зависит от коэффициента пропорциональности, то в осях log/log обе линии буду иметь один и тот же наклон, 45 градусов и параллельный сдвиг. Как видите, понять, что показывает кривая на логарифмических осях, бывает затруднительно.
| рис.19а Световая адаптация глаза. График в линейном масштабе. |  |
Рассмотрим, для чего фотокамере нужны устройства, регулирующие экспозицию (освещенность фотослоя в секунду: лк/с), см. рис.20.
| рис.20 Стандартный бланк и характеристическая кривая (ГОСТ10691.0-84) H ¬ экспозиция фотослоя D – оптическая плотность |
 |
Участок 0-1 — плотность вуали. 1-3 — начальный участок характеристической кривой с непропорциональной передачей яркостей объекта. 3-4 — прямолинейный участок с пропорциональной передачей яркостей, 4-6 верхний участок непропорциональной передачи, 6-7 область соляризации.
| рис.20а Процесс фиксации объектов сцены на фотографическом материале (позитивный процесс). При правильной экспозиции полезный интервал яркостей объектов отображется почти целиком в оптический интервал яркостей фотослоя. Незначительная компрессия сигнала в темной и светлой части фотослоя. |  |
| рис.20бНедодержка. Экспозиция фотослоя недостаточна, светлые детали маскируются шумом фотослоя. Значительная нелинейность передачи градаций. |  |
| рис.20в Передержка. Экспозиция слоя слишком велика, средние полутона чернеют, большая часть деталей в тенях потеряна. |  |
Обратите внимание, что стандартный бланк построен в осях Log-Lin. Сделано это просто для удобства наблюдения за участками характеристической кривой. Заметьте, что изображенный процесс на рисунках 20а,б,в — позитивный. Заметьте также: по оси абсцисс по-прежнему отложен логарифм экспозиции. При этом никакой ошибки между тремя величинами: плотности D, экспозиции H, и интервала яркостей B нет. Это, наверное, трудный момент для понимания, но обо всем на одной странице не расскажешь. И последний момент: ни о какой линейности в передаче яркостей в негативном хим. фотопроцессе не может быть и речи.
Фотослой разрабатывается таким образом, чтобы весь полезный интервал яркостей оказался записан в фотослое. Правильная выдержка характерна тем, что наиболее информативный интервал яркостей попадает на линейный (в логарифмическом масштабе экспозиции) участок характеристической кривой. На рисунках 20б,в показаны ситуации, когда настройка фотоаппарата не совпадает с освещенностью сцены. По аналогии, для глаза можно указать, что рисунок 20а "Правильная экспозиция" соответствует полной адаптации цветного зрения (photopic system), рис.20б "Недодержка" соответствует резкой смене освещенности в сторону уменьшения, и рис.20в "Передержка" — наблюдению за объектом против слепящего света. Здесь важно отметить, что сама характеристическая кривая на всех трех рисунках при этом не меняется, она — конструктивный параметр. Увеличилась освещенность сцены, и человек адаптирует фотоаппарат, уменьшая время выдержки, уменьшая отверстие диафрагмы объектива, и если этого недостаточно, то меняет фотоматериал на менее чувствительный. Аналогично, наша система зрения автоматически уменьшает диаметр зрачка, и перестраивает химический состав фоточувствительного слоя, или даже полностью меняет слой — с колбочек на палочки (конечно не стоит это воспринимать буквально, мы только проводим аналогию). Если мы хотим фотографировать белую бумагу с черным текстом под прямыми солнечными лучами, мы должны адаптировать фотоаппарат к освещенности такой сцены, а наша зрительная система делает то же самое автоматически. Когда мы входим с этим листом в комнату с тусклым освещением, мы снова должны адаптировать фотоаппарат к новым условиям освещения, в то время как зрительная система делает это вновь автоматически. Мы видим по-прежнему белый лист с черным текстом, а фотоаппарат может "увидеть" лист черным. Кстати, по этой причине "на глаз" учесть освещенность и поставить правильно выдержку очень сложно, опытные фотографы скорее анализируют общий вклад источников света в освещенность сцены, чем доверяют глазам. На сегодня для обычных условий съемки всё это уже забыто и вытеснено экспонометрами.
Может ли человек одновременно видеть весь диапазон яркостей в 10млрд. раз одинаково хорошо? Конечно нет, если принять одно только время темновой адаптации, примерно, пусть 5 минут, и световой адаптации, около полутора минут, это уже указывает на невозможность одновременного наблюдения столь большого интервала яркостей. Точно также фотоаппарат, обладая еще худшими характеристиками, чем наш глаз, требует времени на смену фотопленки с другой чувствительностью и на перенастройку времени экспозиции ("время адаптации фотоаппарата"). Простой опыт покажет наличие непропорциональных участков восприятия яркостей: посмотрите на монетку в руке на уровне пояса, а потом на монетку в вытянутой руке возле диска Солнца. Адаптация сработает по мощному источнику света — Солнцу, и детали диска станут неразличимы в потемневшем диске монетки. Куда делись детали? Они перешли в область непропорциональной передачи яркостей. Очень хорошо нам всем знаком и эффект ослепления бликом хромированых поверхностей тел вращения, когда сам блик выглядит не бесконечной острой и малой в угловых размерах точкой, что соответствует физическому распределению яркостей, а вполне приличным по размерам пятном "засветки". Бликовое рапределение яркостей на таких поверхностях (этот вопрос хорошо изучен в программах генерации 3D графики по методу raytracing) обещает нам бесконечно малый размер светящей точки, и это можно подтвердить, если фотоаппаратом сфотографировать эту же сцену, выбрав экспозицию не по средней освещенности сцены, а по максимальной освещенности в окрестности блика. Размер пятна, в фотослое, будет уменьшаться по мере уменьшения экспозиции. Объяснить это можно одним и тем же, для фотоматериала и глаза, проявлением нелинейности, непропорциональной передачей яркостей, когда настройка экспозиции, как и настройка зрительной системы (адаптация), выводит меньший по площади, но очень яркий источник за пределы линейного участка восприятия/экспозиции.
Итак, по аналогии мы можем предположить, что наша зрительная система для одномоментного просмотра имеет характеристическую S-образную кривую, подобную для фотоматериала на рис. 20, на которую как бы откладываются яркости объектов сцены. При таком предположении появляется интересный физический смысл показанной на рис.19, 19а, зависимости. Это хорошо известное из теории линейных систем дополнительное требование к линейным системам: сдвиг по оси сигнала x(t) приводит к такому же сдвигу выходного сигнала y(t). То есть, перемещение вверх-вниз S-образной кривой по секции 3 или 5 освещенности сцены, на рис. 19, не должно искажать форму S-образной кривой. Это в принципе подтверждается многими фактами, например, цвет светового пятна в результате смешения световых пучков не зависит от абсолютностной яркости пучков, а только от их соотношения, константность восприятия цветов и др.
Если для фотоматериала построение кривой рис. 20 представляет лишь технические трудности, то построение с помощью приборов подобной кривой для нашей зрительной системы принципиально невозможно. Мы пока не научились физическими методами измерять ощущения.
| рис.21 Предположительная S-образная кривая характеристической чувствительности зрительной системы человека, B — яркость объектов. Обратите внимание, что график представлен в линейных осях. |  |
Однако у нас есть инструмент под названием логическая машина, которой можно проанализировать работу зрительной системы в нашей гипотезе об S-образной кривой. Мы будем исходить из того факта, что если бы мы сумели изготовить физическое устройство с идеальной линейной передаточной характеристикой, заведомо многократно линейнее нашего глаза и конечно, много линейнее худшего, в сравнении с глазом, фотопроцесса, и воспроизвести на таком физическом устройстве какую-нибудь сцену, то линейное отображение на таком устройстве можно было бы сравнивать с реальной сценой. Тогда, если проверяемое физическими методами исключительно линейное устройство покажет нам точно такое же соотношение градаций, число деталей, четкость, правильность цветопередачи и прочие параметры в сравнении с реальной сценой, то исходя из подобия мы сможем сделать заключение о линейности системы нашего зрения. Если нам захочется где-то что-то подправить в изображении на нашем идеальном воспроизводящем устройстве, скажем, в области теней, в светах или в балансе белого, тогда мы сможем сделать заключение о характере нелинейности системы нашего зрения.
Такое устройство есть. Называется оно зеркало. Это идеальное записывающе-воспроизводящее устройство с практически идеальной характеристикой. Входной сигнал x(t) самое большее, масштабируется с коэффициентом отражения, меньшим единицы. Если вам захочется что-то подправить в таком отображающем устройстве на предмет улучшения изображения, это весьма тревожный сигнал :) значит, вам, наконец, пора выспаться.
Таким образом, мы имеем все данные, чтобы разобрать миф номер шесть: «гамма-компенсация со степенью 1/2.2 необходима для изображений, предъявляемых на мониторе или на бумаге, так как наше зрение имеет тот же характер нелинейности, что и функция гамма-компенсации с рис.6. Или: глаз обладает нелинейностью почти по логарифмическому закону, поэтому, де, и т.д.» Для нашего зрения за образец качества отображения всегда будет выступать линейное зеркальное отображение. Для получения зеркального качества отображения сцены устройство приема-записи-обработки-отображения должно быть идеальной линейной системой.
Кстати, уже после описания предположительной "характеристическую S-образную кривой" я обнаружил точно такую же аналогию в книге кинооператора Железнякова [15]. Где, несмотря на обширный список литературы по цветоведению, он тоже употребляет по отношению к "характеристическую S-образную кривой" слова "по-видимому". Еще позже, на форуме Matlab в дискуссии со мной один из разработчиков примеров для использования Matlab в обработке изображений также вначале указал на S-образную кривую зрения, однако источников вспомнить не смог. Когда он, по-видимому, заглянул в книги, то не смог удержаться на логически верном плато -- и в дальнейшем он указал, что S-образная кривая построена в осях Lin-Log, что превратило эту кривую в логарифмическую на линейных осях, с небольшими искажениями на границах диапазона. Впрочем, автор не смог даже объяснить две из начальных формул в своем "Кратком курсе теории обработки изображений".
В этой главе я постараюсь остаться только в контексте гаммы и гамма-коррекции.
Для того, чтобы понять принцип работы сканера или цифровой фотокамеры, необязательно брать реальное устройство. Множество несущественных деталей можно опустить, без потери принципа. Давайте посмотрим на фотокамеру и сканер, нельзя нам обойтись чем-нибудь одним? Оба устройства фиксируют изображение на плоскости.
| рис.22 Процесс формирования изображения. |  |
Система получает, неважно каким образом, информацию с каждой точки картинной плоскости сцены x1,y1 и отображает ее в картинную плоскость изображения. Разница между фотокамерой и сканером существует в источнике подсветки, оптической системе, в размерах фоточувствительной матрицы и прочих несущественных для принципа деталях. Насчет третьего измерения беспокоится не будем, так как наше зрение тоже "не видит" третье измерение, получая изображение на внутренней стенке глазного яблока, а лишь оценивает его глубину, и делает это пока неясным для нас способом. Выделить четкое физическое соответствие конкретной точки x,y на картинной плоскости объектов каждой точке x1,y1 плоскости изображения не удастся, так как каждая точка x,y будет содержать информацию от точки x1,y1, от ее соседней точки, а возможно, и от всех точек на сцене. Кроме того, в реальности существует проблема и на стороне x,y — это насыщение и "засветка" (не оптическая!) соседних ячеек и интерполяция реальных пикселов в математическую матрицу изображения. Однако предположив, что система формирования изображения линейна, а значит, информация от всех точек накапливается линейно, еще более упростим, посчитаем, что информация точки x,y складывается только из малой окрестности точки x1,y1. Таким образом, чуть-чуть сдвинув картину объектов, сдвинувшуюся картину изображения можно считать изменившейся только в окрестностях точек по границе изображения. Ну вот, вроде все упрощения изложены. Теперь давайте еще упростим устройство получения изображения, указав на равнозначность всех точек перед системой. Мы можем представить, что наше устройство имеет всего одну точку на плоскости объектов и соответственно, одну точку на изображении. Представим, что картинная плоскость протяжённее окрестности точки x1,y1, и вопрос о границе картинной плоскости изображения тоже снимается. В итоге мы имеем устройство с разрешением 1х1 пиксел, и мы понимаем, какие ограничения имеет эта модель.
,............
,.......
Если бы у нас отсутствовал элемент "черный ящик" storage, transmission, processing,.. , между камерой и дисплеем (смотри рис.23), то вопрос в необходимости применения гамма-коррекции внутри камеры отпадает сам собой. Вопрос становится бессодержательным, потому что не имеет значения, вводится гамма-коррекция в камере или в дисплее. Гамма-коррекция нужна, без нее на мониторе мы получим сильно искаженное изображение. Её обязательно вводят перед подачей сигнала на дисплей.
Однако всё круто меняется, если "черный ящик" storage, transmission, processing,.. , существует.
| рис.23 Повтор рис.5 | |
,............
,............
Для иллюстрации того, что происходит с вашим линейно оцифрованным файлом, будь то RAW-data с цифровой камеры, или линейно сканированное изображение (no color corrections, Gamma=1.0), или CGI, я приведу внизу длинную таблицу с числовыми значениями, на этот раз для гамма-компенсации. Гамма-компенсация скрыта от поверхностного взгляда, и находится в профайлах (profile) рабочих пространствах (Working spaces) Adobe Photoshop, в которых значение "гамма" не равно 1.0, например:
|
Приблизительная |
1.8 | 2.2 | 2.2 | 2.2 | 2.5 | 2.5 |
|
Формула, которая |
Y=X1/1.72 | Y=X1/2.22 |  |
 |
 |
|
|
Примеры |
ProPhoto RGB |
AdobeRGB(1998) |
sRGB [14] |
Kodak Photo |
SMPTE-C (PAL) |
Lab |
|
Apple RGB |
CIE RGB |
|||||
|
ColorMatch RGB |
Wide Gamut RGB |
|||||
|
|
Simplified KODAK |
|||||
|
|
SMPTE-C (NTSC) |
|||||
|
x – числовые значения пиксела у – гамма-скорректированные значения пиксела |
||||||
Когда пользователь открывает в Photoshop любой файл, у него только три выбора:
Обойтись без назначения profile в Photoshop не удастся. Но можно создать собственный profile, который вас устроит.
Обратите внимание, что происходит с градациями линейно оцифрованного файла, если к числовым значениям пикселов применяется гамма-компенсация. В последней правой колонке видно, что в тенях градации разрываются, в то время как в средних тонах и в светах отдельные градации начинают компрессироваться в общее ближайшее дискретное значение. Во второй колонке одним цветом выделены дискреты, "сливающиеся" в ближайшее дискретное число при округлении.
|
Первая колонка -- Вторая колонка -- третья и четвертая |
 |
 |
|
| x |  |
 |
 |
| 0 | 0 | ||
| 1 | 20.5427 | ||
| 2 | 28.1508 | ||
| 3 | 33.8479 | ||
| 4 | 38.5764 | ||
| 5 | 42.6945 | ||
| 6 | 46.3835 | ||
| 7 | 49.7501 | ||
| 8 | 52.8632 | ||
| 9 | 55.7705 | ||
| 10 | 58.5064 | ||
| 11 | 61.0968 | ||
| 12 | 63.5617 | ||
| 13 | 65.9168 | ||
| 14 | 68.1751 | ||
| 15 | 70.3469 | ||
| 16 | 72.4412 | ||
| 17 | 74.4652 | ||
| 18 | 76.4252 | ||
| 19 | 78.3267 | ||
| 20 | 80.1744 | ||
| 21 | 81.9723 | ||
| 22 | 83.7241 | ||
| 23 | 85.433 | ||
| 24 | 87.1018 | ||
| 25 | 88.7331 | ||
| 26 | 90.3292 | ||
| 27 | 91.8921 | ||
| 28 | 93.4238 | ||
| 29 | 94.9259 | ||
| 30 | 96.4 | ||
| 31 | 97.8476 | ||
| 32 | 99.2698 | ||
| 33 | 100.668 | ||
| 34 | 102.043 | ||
| 35 | 103.397 | ||
| 36 | 104.729 | ||
| 37 | 106.042 | ||
| 38 | 107.335 | ||
| 39 | 108.61 | ||
| 40 | 109.867 | ||
| 41 | 111.107 | ||
| 42 | 112.331 | ||
| 43 | 113.539 | ||
| 44 | 114.731 | ||
| 45 | 115.909 | ||
| 46 | 117.073 | ||
| 47 | 118.223 | ||
| 48 | 119.36 | ||
| 49 | 120.484 | ||
| 50 | 121.595 | ||
| 51 | 122.695 | ||
| 52 | 123.783 | ||
| 53 | 124.859 | ||
| 54 | 125.924 | ||
| 55 | 126.979 | ||
| 56 | 128.023 | ||
| 57 | 129.057 | ||
| 58 | 130.082 | ||
| 59 | 131.096 | ||
| 60 | 132.102 | ||
| 61 | 133.098 | ||
| 62 | 134.085 | ||
| 63 | 135.064 | ||
| 64 | 136.035 | ||
| 65 | 136.997 | ||
| 66 | 137.951 | ||
| 67 | 138.897 | ||
| 68 | 139.835 | ||
| 69 | 140.766 | ||
| 70 | 141.69 | ||
| 71 | 142.607 | ||
| 72 | 143.516 | ||
| 73 | 144.419 | ||
| 74 | 145.315 | ||
| 75 | 146.204 | ||
| 76 | 147.087 | ||
| 77 | 147.963 | ||
| 78 | 148.834 | ||
| 79 | 149.698 | ||
| 80 | 150.556 | ||
| 81 | 151.409 | ||
| 82 | 152.256 | ||
| 83 | 153.097 | ||
| 84 | 153.933 | ||
| 85 | 154.763 | ||
| 86 | 155.588 | ||
| 87 | 156.408 | ||
| 88 | 157.222 | ||
| 89 | 158.032 | ||
| 90 | 158.837 | ||
| 91 | 159.636 | ||
| 92 | 160.431 | ||
| 93 | 161.222 | ||
| 94 | 162.007 | ||
| 95 | 162.788 | ||
| 96 | 163.565 | ||
| 97 | 164.337 | ||
| 98 | 165.105 | ||
| 99 | 165.869 | ||
| 100 | 166.628 | ||
| 101 | 167.384 | ||
| 102 | 168.135 | ||
| 103 | 168.882 | ||
| 104 | 169.626 | ||
| 105 | 170.365 | ||
| 106 | 171.101 | ||
| 107 | 171.833 | ||
| 108 | 172.561 | ||
| 109 | 173.285 | ||
| 110 | 174.006 | ||
| 111 | 174.723 | ||
| 112 | 175.437 | ||
| 113 | 176.147 | ||
| 114 | 176.854 | ||
| 115 | 177.558 | ||
| 116 | 178.258 | ||
| 117 | 178.955 | ||
| 118 | 179.648 | ||
| 119 | 180.339 | ||
| 120 | 181.026 | ||
| 121 | 181.71 | ||
| 122 | 182.391 | ||
| 123 | 183.069 | ||
| 124 | 183.744 | ||
| 125 | 184.416 | ||
| 126 | 185.085 | ||
| 127 | 185.752 | ||
| 128 | 186.415 | ||
| 129 | 187.076 | ||
| 130 | 187.733 | ||
| 131 | 188.388 | ||
| 132 | 189.041 | ||
| 133 | 189.69 | ||
| 134 | 190.337 | ||
| 135 | 190.982 | ||
| 136 | 191.623 | ||
| 137 | 192.263 | ||
| 138 | 192.899 | ||
| 139 | 193.533 | ||
| 140 | 194.165 | ||
| 141 | 194.794 | ||
| 142 | 195.421 | ||
| 143 | 196.045 | ||
| 144 | 196.667 | ||
| 145 | 197.287 | ||
| 146 | 197.904 | ||
| 147 | 198.519 | ||
| 148 | 199.132 | ||
| 149 | 199.742 | ||
| 150 | 200.351 | ||
| 151 | 200.957 | ||
| 152 | 201.56 | ||
| 153 | 202.162 | ||
| 154 | 202.762 | ||
| 155 | 203.359 | ||
| 156 | 203.954 | ||
| 157 | 204.548 | ||
| 158 | 205.139 | ||
| 159 | 205.728 | ||
| 160 | 206.315 | ||
| 161 | 206.9 | ||
| 162 | 207.483 | ||
| 163 | 208.065 | ||
| 164 | 208.644 | ||
| 165 | 209.221 | ||
| 166 | 209.797 | ||
| 167 | 210.37 | ||
| 168 | 210.942 | ||
| 169 | 211.512 | ||
| 170 | 212.08 | ||
| 171 | 212.646 | ||
| 172 | 213.21 | ||
| 173 | 213.773 | ||
| 174 | 214.333 | ||
| 175 | 214.892 | ||
| 176 | 215.45 | ||
| 177 | 216.005 | ||
| 178 | 216.559 | ||
| 179 | 217.111 | ||
| 180 | 217.662 | ||
| 181 | 218.211 | ||
| 182 | 218.758 | ||
| 183 | 219.303 | ||
| 184 | 219.847 | ||
| 185 | 220.389 | ||
| 186 | 220.93 | ||
| 187 | 221.469 | ||
| 188 | 222.007 | ||
| 189 | 222.543 | ||
| 190 | 223.077 | ||
| 191 | 223.61 | ||
| 192 | 224.142 | ||
| 193 | 224.671 | ||
| 194 | 225.2 | ||
| 195 | 225.727 | ||
| 196 | 226.252 | ||
| 197 | 226.776 | ||
| 198 | 227.299 | ||
| 199 | 227.82 | ||
| 200 | 228.339 | ||
| 201 | 228.858 | ||
| 202 | 229.375 | ||
| 203 | 229.89 | ||
| 204 | 230.404 | ||
| 205 | 230.917 | ||
| 206 | 231.428 | ||
| 207 | 231.938 | ||
| 208 | 232.447 | ||
| 209 | 232.954 | ||
| 210 | 233.46 | ||
| 211 | 233.965 | ||
| 212 | 234.468 | ||
| 213 | 234.97 | ||
| 214 | 235.471 | ||
| 215 | 235.97 | ||
| 216 | 236.469 | ||
| 217 | 236.966 | ||
| 218 | 237.461 | ||
| 219 | 237.956 | ||
| 220 | 238.449 | ||
| 221 | 238.941 | ||
| 222 | 239.432 | ||
| 223 | 239.922 | ||
| 224 | 240.41 | ||
| 225 | 240.897 | ||
| 226 | 241.383 | ||
| 227 | 241.868 | ||
| 228 | 242.352 | ||
| 229 | 242.835 | ||
| 230 | 243.316 | ||
| 231 | 243.796 | ||
| 232 | 244.276 | ||
| 233 | 244.754 | ||
| 234 | 245.231 | ||
| 235 | 245.706 | ||
| 236 | 246.181 | ||
| 237 | 246.655 | ||
| 238 | 247.127 | ||
| 239 | 247.599 | ||
| 240 | 248.069 | ||
| 241 | 248.538 | ||
| 242 | 249.007 | ||
| 243 | 249.474 | ||
| 244 | 249.94 | ||
| 245 | 250.405 | ||
| 246 | 250.869 | ||
| 247 | 251.332 | ||
| 248 | 251.794 | ||
| 249 | 252.255 | ||
| 250 | 252.715 | ||
| 251 | 253.174 | ||
| 252 | 253.632 | ||
| 253 | 254.089 | ||
| 254 | 254.545 | ||
| 255 | 255 | ||
Около 70 градаций в светах потеряны. Немного отличающиеся по яркости пикселы потеряли границу между собой, а вместе с ней и пространственную информацию в изображении. Информация в тенях, с первого взгляда, не теряется, но это при условии, что когда-нибудь, еще до любого последующего преобразования (к нему относится любой пересчет пикселов по аппертуре, например, пересчет размеров изображения по bicubic, фильтры unsharp mask, find edges...) будет произведена операция, обратная гамма-коррекции. Если же пересчет пикселов по аппертуре был произведен, то последует потеря информации и в тенях.
Самые тяжелые последствия гарантирует конвертация в Lab, с эквивалентной гаммой 2.5, далее в порядке уменьшения ущерба: гамма 2.5, гамма 2.2, и гамма 1.8.
Не имеет значения и то, производите вы гамма-компенсацию в 8-битном представлении или предварительно конвертируете имеющиеся 256 значений в 16 бит. Результат будет точно такой же. Если АЦП вашей видео/фотокамеры/сканера имеет внутренний формат 8 бит (что должно иметь место, рассматривая многие среднего уровня камеры), то внутренняя конвертация в 16 бит даст всего лишь бессмысленную двойную точность описания для тех же 8 бит. Такова природа дискретных сигналов. Еще одну вещь стоит напомнить, что Adobe Photoshop при открытии файла 16 бит (диапазон градаций 0-65535) прежде всего конвертирует данные в 15+1 бит (диапазон градаций 0-32768), где один бит используется под знак. При записи в файл он снова конвертирует в 16 бит. В принципе, это несущественно, если вы не выполняете пару десятков преобразований с этим файлом в Adobe Photoshop. Некий Chris Cox (его имя есть в заставке Adobe Photoshop) в небольшой дискуссии пытался сохранить хорошую мину Adobe при плохой игре.
Из этой таблицы хорошо видно, что если вы владелец цифровой фотокамеры с возможностью получать RAW-данные, или владелец сканера, позволяющего получать RAW-данные, и в тоже время сохраняли оцифрованные файлы изображений конвертированными из RAW-данных в любой профайл с гаммой 2.2 или 1.8, то ваши конвертированные файлы оптимизированы для просмотра на мониторе, но более никуда не годятся — ни для серьезной работы в полиграфии, ни для качественной печати на фотопринтерах, ни для использования в программах рендеринга, ни просто для архивных целей. Эти файлы потеряны.
Итак, самые тяжелые последствия приносит миф номер семь: «гамма-компенсация, вводимая как трансформация числовых значений пикселов, дает улучшение качества воспроизведения теней, светов и пр.»
Q: какой смысл во всём сказанном, если я не вижу на мониторе никакого ухудшения после конвертации в профайл с гамма-коррекцией?
A: естественно, что на хорошем оригинале реальной сцены не видно потерь, происходящих, например, при конвертации RAW -> Lab. Если был проведен тест с постеризацией (menu: Layer>New Adjastmens Layer>Posterize) этого же оригинала, как было описано выше в разделе 2.3, то можно заметить, что потеря половины градаций также не сильно влияет на визуальное качество изображения на мониторе. Все артефакты от потерь в градациях увидите позже, когда проведете коррекцию изображения для своих нужд и конвертируете в профайл оконечного устройства.
Reference:
1.
2. Steve Mann. Comparametric Equations with Practical Applications in Quantigraphic Image Processing. IEEE TRANSACTIONS ON IMAGE PROCESSING, VOL. 9, NO. 8, AUGUST 2000 [offline(75K), только страницы 1389-1392]
3. ITU-R Recommendation BT.709, Basic Parameter Values for the HDTV Standard for the Studio and for International Programme Exchange (1990), [formerly CCIR Rec. 709], ITU, 1211 Geneva 20, Switzerland.
4. http://www.ukl.uni-freiburg.de/aug/mit/bach/ops/crtlimits.html
5. http://www.brucelindbloom.com/DanMargulis.html
6. Hurvitch (Hurvich) L.M., Jameson D., The Perception of Brightness and Darkness, Boston: Allyn and Bacon, 1966
7. Cornsweet, T. Visual Perception. Academic Press, New York, 1970.
8. И.М.Журавель. Модель зрительного восприятия света человеком и ее использование при создании методов обработки изображений http://www.matlab.ru/imageprocess/book2/1.asp
9. Основы ФПМ ПЗС для высококачественного формирования изображений http://www.ssga.ru/metodich/ph_ccd/00_index.html
10. Г.Г.Гинкин. Справочник по радиотехнике. изд.4, перераб., Государственное Энергетическое Издательство: Москва-Ленинград, 1948.
11. Устройство цветных кинескопов. Курс лекций. http://www.do.sssu.ru/virt/library/uchebnik/tv/colkin5.html
12. Dr. Victor Zamyatin's Personal Web Site. Dark Adaptation. http://wmed.narod.ru/w_ophth/physiol/ph_03.htm
13. Dr. Victor Zamyatin's Personal Web Site. Light adaptation. http://wmed.narod.ru/w_ophth/physiol/ph_02.htm
14. M.Nielsen, M.Stokes. The Creation of the sRGB ICC Profile. http://www.srgb.com/c55.pdf, http://www.srgb.com/srgbgammacalculation.pdf
15. http://www.ezhe.ru/data/vgik/zhv-cvet_kontrast_3.html
